Grupo Miércoles
Problema
La geometría del material que obtenemos a partir de la traducción de las imágenes binarias en propiedades mecánicas es tan solo una celda unitaria que al ser teselada en las dos direcciones del espacio 2D conforma un material periódico en una escala superior. Considerando esto, requerimos de una herramienta o algún método que permita imponer condiciones de frontera periódicas en nuestra celda unitaria al momento de resolver con FEM para así tener congruencia con el modelo material que estamos simulando.
Desarrollo de la reunión
- Se propone como solución explorar el uso de Multi-Point o Multi-Freedom Constraints, las cuales consisten en ecuaciones adicionales que se añaden al sistema matricial del problema elástico. Recordemos que este sistema inicialmente lo podemos escribir de la siguiente manera:
Donde $[K]$ es la matriz de rigidez del sistema, ${U}$ es el vector de desplazamientos y ${F}$ el vector de fuerzas. Utilizaremos elementos de tipo barra para las simulaciones FEM, por lo que cada uno de los nodos de nuestra malla tiene asociados 2 grados de libertad (ó DoF por sus siglas en inglés); uno en la dirección $x$ y otro en la dirección $y$. Para nuestro caso particular, esto implica que si realizamos el análisis FEM para una geometría con 64x64 elementos, el número de nodos en cada una de las direcciones del material sería de 65 (uno más que el número de elementos en cada dirección) y el número de DoF globales sería de $65*2=130$.
Las condiciones de restricción adicionales a este sistema se usan para dar coherencia a la condición de periodicidad del problema. Lo que hacemos con estas condiciones es, por ejemplo, asociar los grados de libertad de la pared izquierda de nuestro material con los grados de libertad de la pared derecha, de modo que imponemos que el desplazamiento de este último conjunto de nodos sea igual (o con una constante adicional, $\varphi$ de diferencia) al conjunto que se encuentra en el lado opuesto de nuestra geometría. Esta asociación de grados de libertad también se impone entre los nodos inferiores y superiores, al igual que entre el nodo de la esquina inferior izquierda y el de la esquina superior derecha. Los nodos internos no son restringidos por ninguna ecuación.
Si generalizamos de forma matemática, podemos valernos de la constante de periodicidad de nuestra celda unitaria, $a$, para escribir estas nuevas ecuaciones como se presenta a continuación. Se utilizan los subíndices $L, R, B$ y $T$ para denotar a los lados a los que pertenecen los desplazamientos (left, right, bottom y top).
- Asociación de desplazamientos izquierda-derecha:
\(u_L(x,y) = u_R(x+a,y) + \varphi\) \(v_L(x,y) = v_R(x+a,y) + \varphi\)
- Asociación de desplazamientos izquierda-derecha:
\(u_B(x,y) = u_T(x+a,y) + \varphi\) \(v_B(x,y) = v_T(x+a,y) + \varphi\)
- Asociación de desplazamientos esquina inferior izquierda-esquina superior derecha:
\(u_{BL}(x,y) = u_{TR}(x+a,y+a) + \varphi\) \(v_{BL}(x,y) = v_{TR}(x+a,y+a) + \varphi\)
Esto anterior es ejemplificado más claramente con la siguiente imagen:
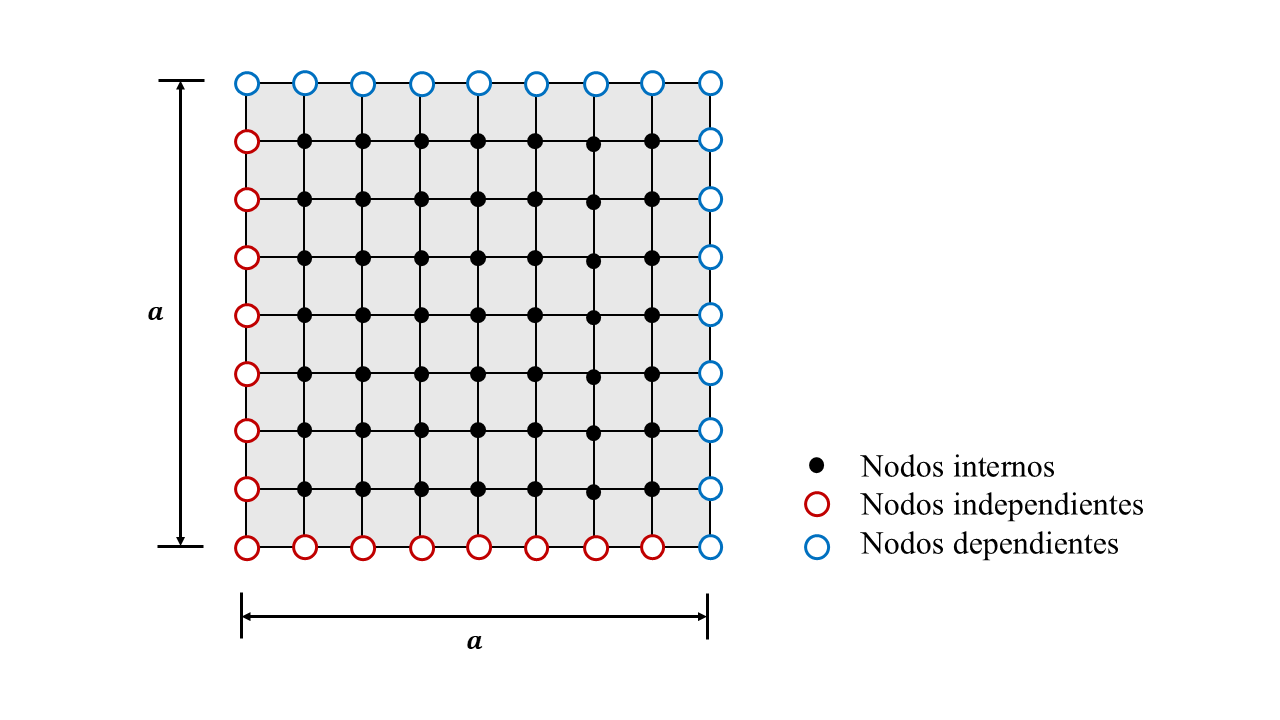
En últimas, estas ecuaciones adicionales causan la reducción del sistema matricial, donde se puede utilizar un solucionador lineal para hallar nuestro nuevo vector de desplazamientos reducido, ${ U_R }$. El nuevo sistema se ve así:
\[[T] [K] [T^T] \{U^* \} = [T] \{F\}\]Donde $[T]$ es la matriz que aparece de la siguiente interpretación:
\[U = T U^*\]Donde $U$ es el vector de desplazamientos del sistema original y $U^*$ es el vector de desplazamientos reducido, que contiene la información de los desplazamientos de nodos internos, $U_{int}$, y de los nodos independientes, $U_{ind}$;
\[U^* = \begin{bmatrix} U_{int} & U_{ind} \end{bmatrix}\]De modo que la matriz T guarda la información de las asociaciones de grados de libertad de los desplazamientos dependientes con sus respectivos nodos en los desplazamientos dependientes:
\[T = \begin{bmatrix} I & 0 \\ 0 & I \\ 0 & U_{dep}^X \\ 0 & U_{dep}^Y \\ 0 & U_{dep}^{XY} \end{bmatrix}\]Compromisos Futuros
- Escribir la rutina en Python que permite calcular la matriz $[T]$ de nuestro problema, con base en unas condiciones de frontera periódicas establecidas.
- Considerando que estamos trabajando con un material compuesto, donde debemos elegir dos materiales que lo forman ¿Cuáles serán las propiedades mecánicas que emplearemos para dichos materiales?